AI Research & Data Scientist
Software Engineer
2024-05-28
Given a problem, what is the best algorithm to solve the problem? This is a seemingly simple question that automated algorithm selection addresses. In this post I will briefly motivate and show how it can be useful to solve problems more efficiently.
Let's say you need to sort many lists. What sorting algorithm should you choose to sort them most efficiently? To keep it simple, let's look at two options -- quicksort and insertion sort. Quicksort is considered the fastest and has the average performance of \(O(n \log(n))\). Insertion sort is on average much less efficient and has an average performance of \(O(n^2)\).
It's tempting to just pick quicksort for all lists because it is generally the fastest algorithm. However, if a list is already sorted or nearly sorted, then the insertion sort will simply scan the array and finish. Therefore, it has a linear time complexity (i.e., \(O(n)\)) on sorted arrays. Quicksort is generally the fastest but is outperformed by insertion sort on already or nearly sorted lists. So, it seems that even for simple problems like sorting there exist complementarity in the performance of algorithms.


Now let's say that you need to solve problems that are harder than sorting, e.g., Sudoku. If you pick a standard 9 x 9 board that is somewhat prefilled, it is not a very difficult puzzle. But what about a general case of Sudoku with n x n board? It turns out that the Sudoku problem in a general case is NP-complete. In simple words, it means that we don't know if there exist algorithms that can solve these problems efficiently in a general case.
Another aspect of NP-complete problems is that they can be quickly reduced (or transformed) to other NP-complete problems. One of the most famous such problems in artificial intelligence is Boolean Satisfiability, or SAT for short. The problem asks: given a Boolean formula (formula where all variables can be either True or False), are there assignments to variables such that the formula evaluates to True? SAT has many applications in practice ranging from mathematics to software and hardware verification to operations research. Coming back to Sudoku, one can reduce the original Sudoku problem to SAT, solve the SAT representation and then convert the solution back to the Sudoku form.
In theory, SAT is a difficult problem, but in practice we can solve many SAT problem instances quite well thanks to the work of many computer scientists. Let's take a look at two of such algorithms from one of the tracks in the 2018 SAT competition. The dataset contains 8 algorithms but I will show only 2 for simplicity.
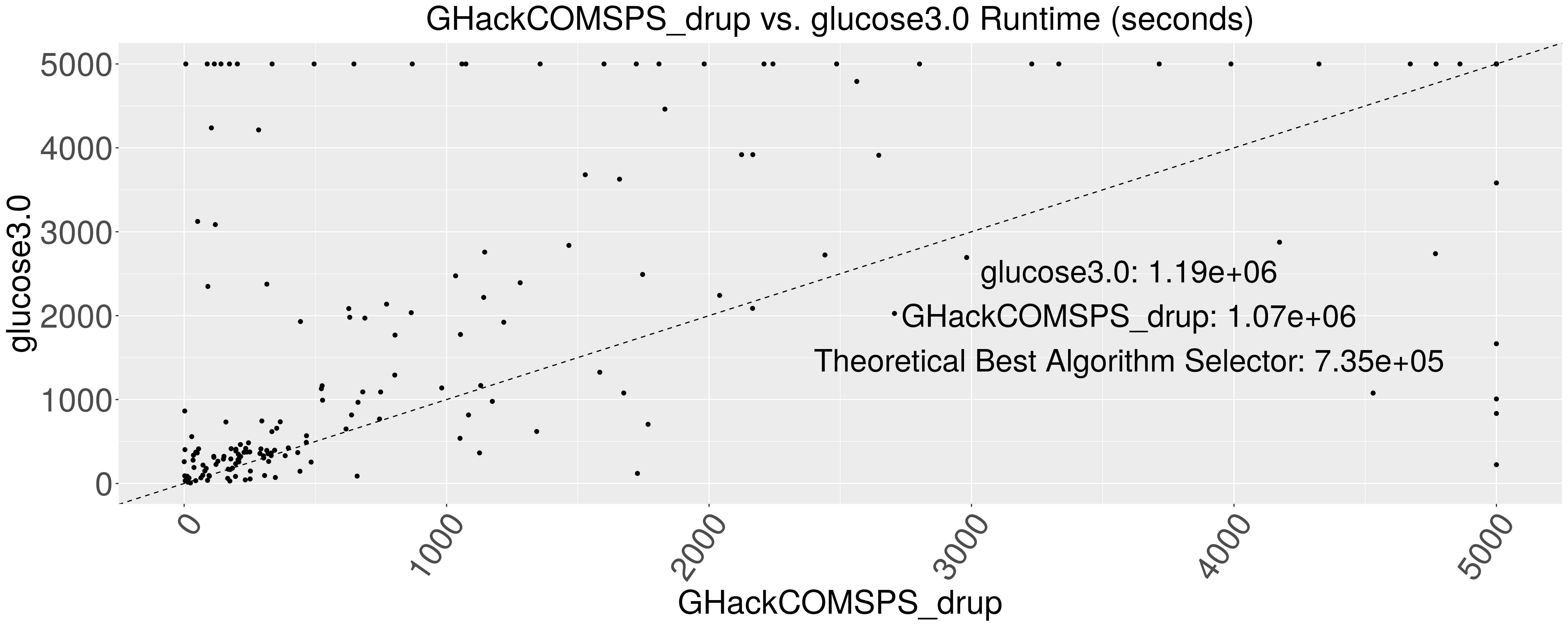
The figure shows two algorithms -- GHackCOMSPS_drup and glucose3.0. I show these two because they are the best and the worst on average in the competition's track. The algorithms are run on 353 problem instances represented by a dot in the figure. Both algorithms terminate after 5000 seconds. The dashed diagonal line is the line of equal performance. If a particular problem is close to the diagonal line, both GHackCOMSPS_drup and glucose3.0 solved that problem instance within the same amount of time. From the figure we see that it is rarely the case. You can also see the total runtime on all problems in seconds for both algorithms.
The image shows that the two algorithms exhibit complementary performance. We see most problems are in the top triangle formed by the dashed line. The points in the top left are the problems solved by GHackCOMSPS_drup within a few seconds but took longer on glucose3.0. But there are dots in the bottom right as well. These are the problems where the glucose3.0 algorithm outperformed GHackCOMSPS_drup, even though it is the worst of the two algorithms.
If you don't know about automated algorithm selection techniques, it's intuitive to just pick GHackCOMSPS_drup to solve all problems since it is the best algorithm on average in this particular case. If we do that, we can solve all problems 118929.9 seconds faster than always choosing glucose3.0, the worst algorithm. This translates to about 33 hours of saved time.
What happens if we leverage all 8 algorithms (note that I only show 2 in the figure) and select the best for each problem instance? Meaning, what happens if we automatically always use the best tool for every problem at hand?
The theoretical best algorithm selector from the figure shows what would have happened if we could automatically select the best possible algorithm for each problem. So, what would have happened if we built the perfect algorithm selector? If we could do that and compare it to always using GHackCOMSPS_drup, then we could save an extra 335027.8 seconds which is an additional 93 hours of saved time!
This example shows that algorithm selection could theoretically be used to solve hard AI problems such as Boolean Satisfiability more efficiently. And since it can help solve Boolean Satisfiability faster, it could also translate to other hard problems such as the Travelling Salesman Problem, Sudoku and others.
The same techniques described here have been used successfully in industry, e.g., in machine learning. The problem of selecting and configuring of models is very important in machine learning and is addressed by automated machine learning (AutoML). Both Amazon and Microsoft offer AutoML services that help software engineers, data scientists and non-technical people to apply ML to their problems by simplifying and automating model selection and hyperparameter configuration among many other things. There are also open-source AutoML software libraries such as auto-sklearn and AutoGluon.
I will only mention one of the popular techniques in automated algorithm selection.
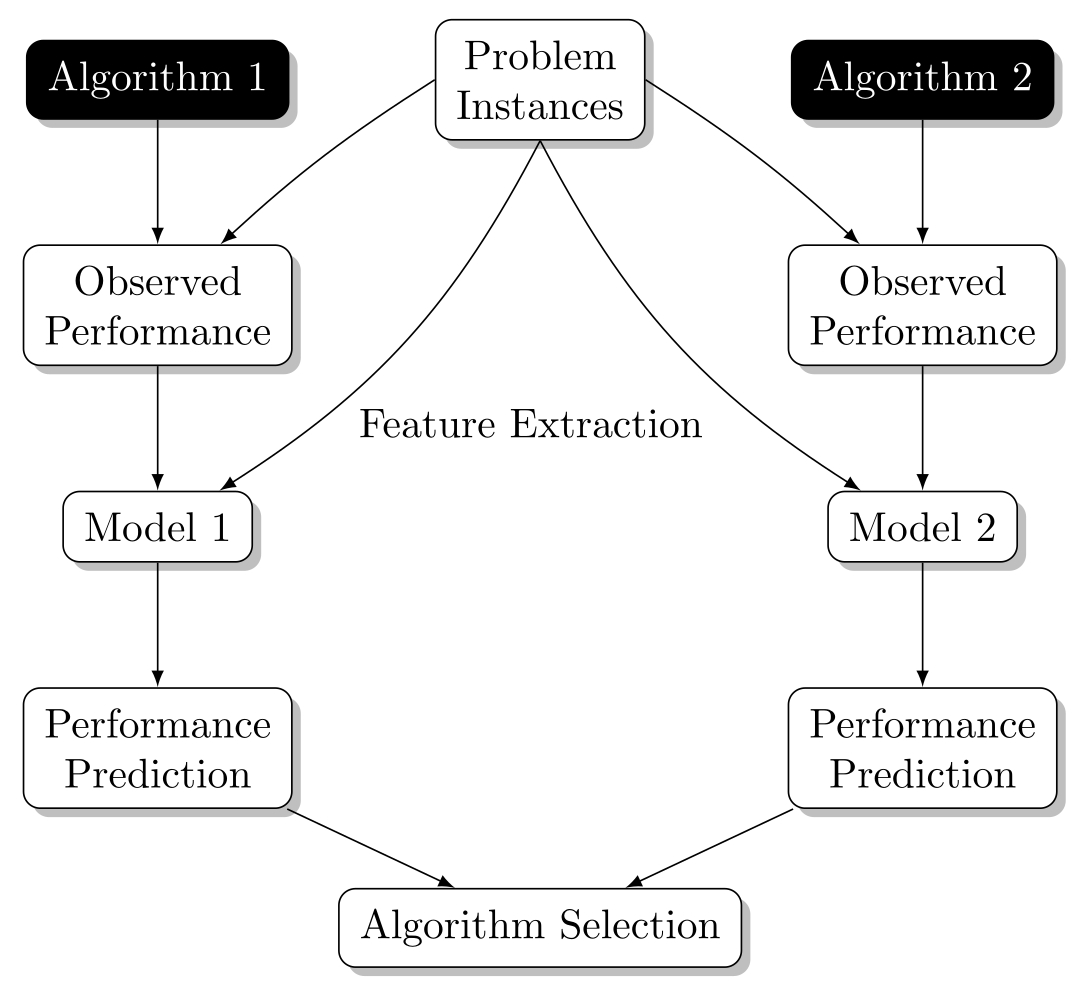
The idea is to build a machine learning model for each algorithm that predicts the performance of the corresponding algorithm. The model trains on the past performance (e.g., runtime) of the algorithm and the features of the problem. In the case of SAT, the features could be properties like the number of Boolean variables as well as more sophisticated features. For Sudoku, features could be things like the size of the board or the percentage of the board already prefilled. The features allow the underlying machine learning models to distinguish between different problems and possibly find patterns in how different algorithms handle different kinds of problems. After obtaining predictions of each algorithm's performance, we can facilitate algorithm selection by simply picking the algorithm with the best predicted performance.
Take a look at the summary of the method in the figure below (taken from one of my own publications). I show only two algorithms for simplicity but in practice there could be a dozen algorithms in a dataset.
There exist open-source software libraries and datasets to facilitate algorithm selection experiments. On the software side, I show the use of the ASlib and LLAMA R language software libraries that help run algorithm selection experiments. I obtained one of the SAT dataset from the aslib_data GitHub repository that contains many algorithm selection datasets from many domains. In the dataset, there are 8 algorithms and they are run on 353 problems. Note that the example with GHackCOMSPS_drup and glucose3.0 showed was a subset of the dataset.
The R code below downloads and prepares the algorithm selection dataset (also known as scenario), creates a random forest learner, adds feature imputation and builds an algorithm selector like the one described in the previous section.
library(mlr)
library(llama)
library(aslib)
sc = getCosealASScenario("GLUHACK-2018")
data = convertToLlamaCVFolds(sc)
learner = makeLearner("regr.ranger")
learner = makeImputeWrapper(learner = learner, classes = list(numeric = imputeMean(),
integer = imputeMean(), logical = imputeMode(),
factor = imputeConstant("NA"), character = imputeConstant("NA")))
model = regression(regressor=learner, data=data)
All this talk is just for a few lines of code!
I ran the code from the previous section on my machine. Take a look at the performance comparison between GHackCOMSPS_drup and a simple algorithm selection system.
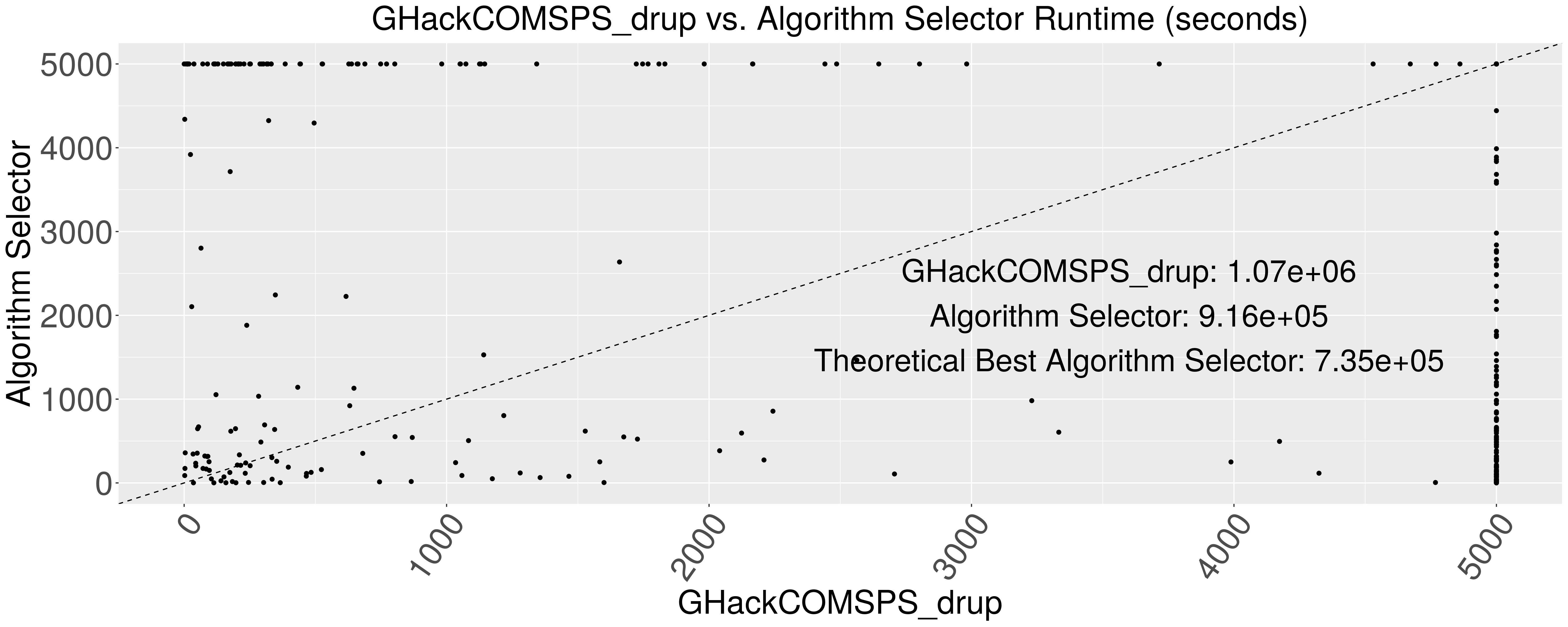
When I compare the results of a simple algorithm selector vs. only running GHackCOMSPS_drup and compute the total runtime of both the selector and GHackCOMSPS_drup I get a total improvement of 153391.8 seconds. This is roughly 42.6 hours in saved compute time! This translates to an additional 108 problem instances that got solved thanks to the simple algorithm selection system. All problems in the far right side of the figure are the problems that were solved by the selector and not by GHackCOMSPS_drup.
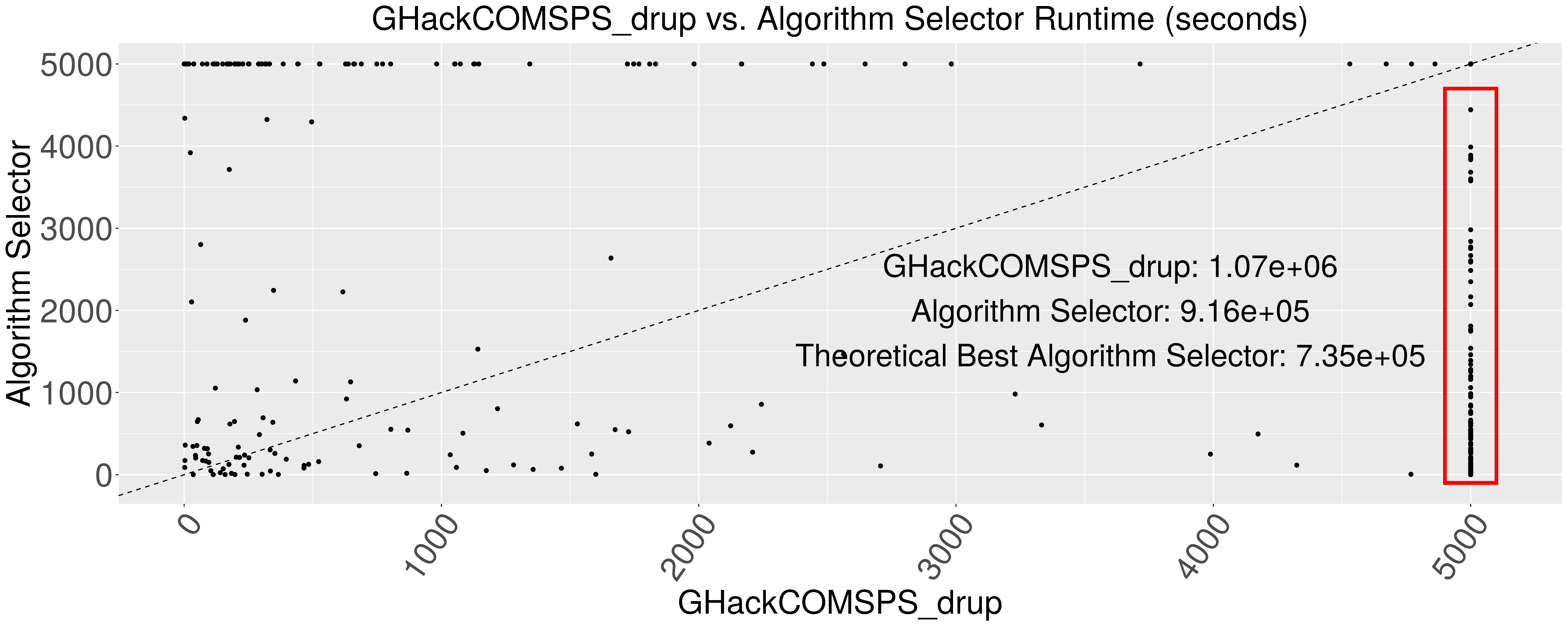
While impressive, our algorithm selector is still 50.4 hours away from achieving the best possible system performance. So there is still room for improvement if we invest more time into this.
We get all these improvements without writing our own algorithm -- we're simply building a machine learning model that picks existing algorithms. And we do it with random forest without any hyperparameter tuning or feature selection!
There is much more to algorithms selection than what I described in this post. If you would like to dive deeper into it, this is a good talk that describes algorithm selection and similar approaches to getting the best performance out of existing algorithms.
If you would like to learn how to use the open-source libraries for this, take a look at the documentation for the LLAMA software library. Also, the aslib_data repository on GitHub has many datasets to get started with coming in from different domains in AI.
If you have a problem domain where there exist complementarity in the performance of algorithms, take a look at automated algorithm selection. This may enable you to solve your problems more efficiently by simply leveraging the strengths and weaknesses of existing algorithms!